Rough surface generation

The characterization of a rough surface can be done with respect to its spatial frequency content. This can be transformed into a constructive method by using a sum of trigonometric functions similar to a Fourier series. Each term in such a sum represents a certain frequency of spatial oscillation.

In Pyrough, a discrete set of spatial frequencies \(\nu_x = a\) and \(\nu_y = b\) (where \(a\) and \(b\) are integers) is used to rationalize the range of investigated frequencies. \(A\) and \(B\) are defined as the respective high-frequency cutoffs for \(a\) and \(b\) so that \(a \in [-A;A]\) and \(b \in [-B;B]\). Thus, the shortest wavelengths are \(\lambda_{x,min} = \frac{1}{A}\) and \(\lambda_{y,min} = \frac{1}{B}\) along \(\vec{u_x}\) and \(\vec{u_y}\) directions, respectively. \(a\) and \(b\) can be positive or negative to ensure oscillations in both directions. A rough surface \(h(x,y)\) can be described by a sum of elementary waves as,

\[h(x,y) = \sum_{a=-A}^{A} \sum_{b=-B}^{B} \alpha_{a,b}cos[2\pi(a x + b y) + \phi]\]

where \(\alpha_{a,b}\) is the associated amplitude to each elementary wave.

Two more contributions are made in order to allow Pyrough to generate self-affine rough surfaces that are randomly perturbed. First, the phase is randomly perturbed using \(\phi = U(a,b)\) where \(U\) states for a uniform distribution on an interval of length \(\pi\). Also, random perturbations and self-affine aspects are implemented within \(\alpha_{a,b}\). One can for example choose \(\alpha_{a,b}\) as a zero-centered Gaussian distribution to get a smooth but random variation in amplitudes without constraining the magnitude i.e., \(\alpha_{a,b} = G(a,b){(a^2+b^2)}^{-(1+\eta)}\) where \(G\) states for a reduced centered normal law and \({(a^2+b^2)}^{-(1+\eta)}\) traduces the self-affine aspect of the surface. Finally, the construction of a randomly perturbed self-affine surface can be modeled as,

\[h(x,y) = C_1\sum_{a=-A}^{A} \sum_{b=-B}^{B} G(a,b) (a^2+b^2)^{-(1+\eta)} cos[2\pi(a x + b y) + U(a,b) ]\]

in which \(\eta\) allows to monitor the roughness degree and \(C_1\) is a normalization factor introduced to fit the surface heights to the sample dimensions.

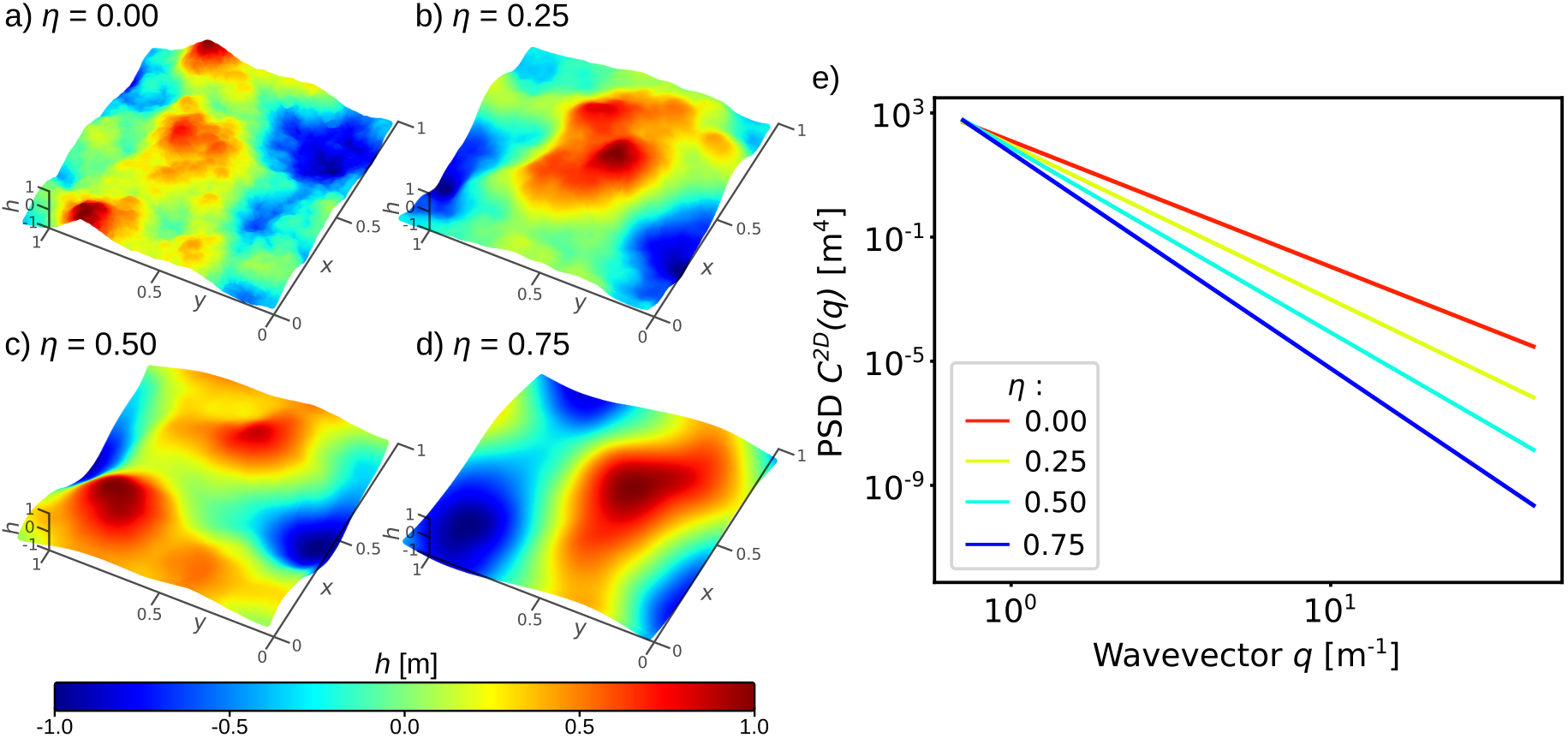
Random numerical self-affine rough surfaces for various Hurst exponents. a) \(\eta = 0.\), b) \(\eta = 0.25\), c) \(\eta = 0.50\), d) \(\eta = 0.75\), e) PSD of the various h profiles. For all calculations, A=50, B=50 and h(x,y) values are normalized between 1 and -1.